Wanting Is Not Weird
“Wanting” may be considered slightly weird to attribute to an arbitrary system, or at least not necessarily a given. For example:
Okay, so you know how AI today isn't great at certain... let's say "long-horizon" tasks? Like novel large-scale engineering projects, or writing a long book series with lots of foreshadowing?
(Modulo the fact that it can play chess pretty well, which is longer-horizon than some things; this distinction is quantitative rather than qualitative and it’s being eroded, etc.)
And you know how the AI doesn't seem to have all that much "want"- or "desire"-like behavior?
(Modulo, e.g., the fact that it can play chess pretty well, which indicates a certain type of want-like behavior in the behaviorist sense. An AI's ability to win no matter how you move is the same as its ability to reliably steer the game-board into states where you're check-mated, as though it had an internal check-mating “goal” it were trying to achieve. This is again a quantitative gap that’s being eroded.)
Well, I claim that these are more-or-less the same fact. It's no surprise that the AI falls down on various long-horizon tasks and that it doesn't seem all that well-modeled as having "wants/desires"; these are two sides of the same coin.
Philosophically, {values, utility, “wants”, preferences} are often considered synonyms to some degree. This is usually not considered controversial, so I am going to start with at least this assumption. Mathematically, the term “utility” is often preferred.
What is “utility”? The von Neumann–Morgenstern (VNM) utility theorem says that rational agents under conditions of uncertainty make decisions by maximizing the expected value of some kind of utility function. You probably know that already if you’re smart.
But how does an agent “get” a utility function? This theorem doesn’t bother to answer that question.
Von Neumann and Morgenstern started with easier things to define utility functions over, such as games. With those, it can be assumed fairly reasonably well that agents generally prefer to win games over losing them. But that merely hints at how agents acquire utility functions, it does not explain in full generality how they come to be or what they come to be.
There’s another question, too: Are you literally a utility function? Or can you simply be modeled as having one? For this question, I fortunately have some thoughts about how to answer this.
Generally speaking, we model agents as - at least since the deep-learning era - as a black-box function of some kind, in full generality. This black-box function simply takes inputs and converts them into outputs. The outputs get sent into the environment, which returns new inputs. There is no explicit “utility function” here.
But you could make it explicit, if you wanted to. What if you instead had a value function, V(x), a function from the same input space to a real value? In this case, it would have to be possible to simulate changes to the input space based on possible actions that could be taken. Assuming one knows how to change the environment’s state to a new state, one could perform a search over all available actions and choose the one that best maximizes expected utility - in this case the function V(x) itself.
If there were an environment that only had sparse rewards, such as a zero-sum game, such a value network may learn to approximate the expected utility of each game state, such that states closer to winning have values closer to 1, and vice-versa. And fortunately, this fact makes it possible to transform a policy network P(x) - a mapping from states to actions (or states to states, if you think of an action as causing the state to become a new state) - back into a value network.
One can think of a policy network as essentially the most general machine that transforms states to states. But a policy network does not explicitly have “preferences” per se. However, a policy network usually outputs a probability distribution over states for a given input state. This probability distribution reflects the prediction of the model for what the next state is going to be. In this case, one can think of the model as essentially considering itself a part of the environment it exists in. Intuitively, the way that the state trajectory propagates forward is, in a sense, what is “preferred” by at least one important aspect of the environment (the agent, which is part of our ontology for modeling the system).
If one wanted to directly compute values for each state that could be reached from some starting point, one could simply perform Monte Carlo rollouts of the policy network by sampling states from its output (perhaps with some noise, if it happened to output only one action per state), and then record counts of each time each state had been reached. The normalized counts could then be used as the values that would be assigned by the policy for each state.
Successful attempts at training neural networks to play games have been based on this premise, such as a technique called Deep Q-Learning.1
In a certain sense, this seems to imply that if I can model my environment more successfully by including “agent-like” processes in my ontology, I could also model such agent-like processes as having “preferences.”
Jessica Taylor mentions this concept in her post The Obliqueness Thesis, in the section titled “Belief/value duality.” This section essentially notes that the behavior of two agents with different utility functions could be made identical by modifying the belief states by an appropriate factor, and vice-versa.
To provide another illustration, imagine a system / agent that is capable of making predictions about another system, in one of two ways:
The agent is outside of the system it wishes to predict, and its outputs do not affect the system at all.
The agent is embedded inside the system it wishes to predict. In this case, its output is part of the system it wants to predict. Therefore, by making a prediction, it is making a prediction about its own output, which is essentially a preference.
We have shown at least several potential ways that an agent can be defined either by a utility function or by making predictions about the future state of the world it’s embedded in, which in some way are dual to each other.
In some fundamental way, then, having preferences shouldn’t be considered very weird.
At Attempt to Define Agents Reductively Via Minimal Tasks
The main bulk of this post is my attempt to hack away at the problem incrementally, beginning with thinking about “tasks” as the atomic unit of interest. In no sense is this guaranteed to be the only way to look at the problem. But I found this method particularly interesting, because it gave way to the kind of duality I was looking for almost immediately.
What if we began with a perspective that says that “agents” are things that “accomplish tasks”? What are the minimal set of “tasks” that we must start with?
One can immediately see we will need a “quality assessment task”, as each task has to be “performed”, but one does not initially know either what needs to be performed, nor even what constitutes “performed”, yet.
We’ll note that one can still be capable of determining whether a given task has been “adequately performed” according to the standards applied within the locality of the task, which may consist of another agent actually undertaking it. Even if the agent not undertaking said task does not immediately consider that task necessary for itself to do right now, it can still understand what would constitute necessary as well as adequate from the perspective of the other agent.
We’ll initially think of the quality assessment task as the thing we want to show is equivalent to utility or “values.” As well as the thing that most agents start with, the only thing they really know from the outset.
But we also notice that, self-reflectively, even by just trying to define what tasks we need, we must also be pointing at some kind of “task separation” task. We will call the first task - the “quality assessment task” - “J”, and the “task separation task” will be called “T”.
“yes” : J generally means that I expect whatever the “yes” points at to reappear at some point.
“no” : J generally means that I expect whatever the “no” points to not to reappear.
These judgement calls are not - and can’t be - judgements of certainty, and in fact we do not yet have any notion of what certainty means. These, for now, are merely fuzzy notions of better and worse. In fact, since each instance of J can be applied to a previous instance of J, this is the only way that greater and less certainty can be constructed.
My opinion is that J is kind of special: It’s kind of both dual to T as well as equivalent to T, when it operates on itself (big big claim). So J is just a tad more of a predecessor to T. I think this potentially resolves the issue of “why do we start with two objects right away?”
Here’s an intuitive summary of my argument that will be proceeding from here: T and J, first of all, must be somewhat related or entangled. Precisely how has yet to be determined. But one thing we do know is that J is used to determine how well tasks are performed. So that means one cannot really do T without J.
Suppose that I wanted to “judge” (an instance of J) a certain task K. To do this, I assign “yes” to some instances of K and “no” to others. This innately splits tasks into two varieties. Equivalently, I notice that task K is sometimes done as “K_1”, and other times as “K_2.” Noting that K_1 gets performed more frequently than K_2, I consider K_1 > K_2 for now. This was an instance of J, as well as task T, because I separated task K into K_1 and K_2.
But, this J was also an instance of “J^2”, which means J applied to itself. In the next more thorough attempt at argument, I’ll show why this is in more detail.
An Attempt At Formal Argument That T = J^2
In this argument I will be using the word “proof” in a somewhat grandiose manner, but keep in mind that this is mostly an attempt at something like informal proof, so I would ask that you please bear with me. Every time you see the word “proof” you can replace that in your mind with “an attempt to argue rigorously, even though the adequate level has yet to be achieved here.”
This formality begins with a bit of informality, which we then show to be a possible pathway towards formality in the following way: We presuppose that "society" is defined by a collection of tasks which are performed by task-performers. We are luckily able to define two tasks from this immediately, in a straightforward manner: One task will be called Task-Delineation, and is defined to be the task of task-definition itself. The second task will be called Judgement, and is the task of assigning approval and disapproval to arbitrary task outputs. These two tasks are necessary inclusions into the initial task set. From this, it is immediately clear that task-delineation itself was performed in order to generate these two tasks. It is also clear that judgement has been performed to assess the quality of this delineation. This is good, because for our theory to be correct, it must be capable of describing itself. This last step was an instance of what we call J^2, or judgement applied to itself. Judgement can be applied to anything, which means it can be applied to itself. We also note that it is used to determine how well task-delineation is performed, so it must be a component of that task as well.
Task Delineation (Task T): A task is a process which is intended to accomplish an objective. Task Delineation is defined to be the task of describing, defining and discriminating between various tasks themselves.
Judgement (Task J): The task defined with the objective of quality determination. It takes task output as input and produces approval and disapproval as a task output.
A natural question which arises is whether or not we need to actually define any new tasks besides these. The answer is that for our proof of T = J^2, no specific tasks are necessary to define besides the ones we already have. That being said, we do need to use letters to refer to additional “dummy” tasks that could be defined. We will typically use letters close to T alphabetically to stand for variable tasks, e.g., (Q, R, S, T, U, V). These are tasks which are assumed to be "close" to task T in some way. Task J is not usually placed in the list of tasks like these, because it is assumed that task J will apply to all tasks. That is, any task will require task J to be applied to it in order to be performed adequately.
We can represent task J being applied to task T like so:
It is also the case that T itself is composed of T and J:
Note that the above also is an instance of task-delineation, which decomposes T into T and J, and denotes that J applies to T. We also represent that J may apply to itself, sometimes with a looped arrow (which is quite hard to type-set).
Note that J^2 will also be used to denote J with the arrow pointing back down to itself, both meaning J applied to itself. The reason for this level of distinction between J and J^2 is because J is not necessarily applied to itself at all times. In full detail, the relationship between T and J is as follows:
This much is not yet enough for us to conclude that T = J^2. In order for us to do this, our theory must be self-reflective and self-representational enough for us to conclude that we are, in fact, using pieces of it or doing pieces of it while we reason about it. For example, this section itself must qualify as performing task T, as we have defined it. Therefore, by the end of the proof, we must be able to conclude that we are also performing J^2.
Task-Delineation is equivalent to Judging-Judging.
First we have to define what "well" means. Suppose we have a collection of Judgers (J-doers). These Judgers judge mainly the quality of doers at other tasks. (Doers can be considered other doers, or alternatively other instances of doing, such as the same doer who performed attempts of tasks in the past.) These judgements are reflected in the positivity or negativity of the expressions emitted by a J-doer at the output of a task-doer. We may not know, as of yet, whether or not these judgements have anything at all to do with the actual quality or performance of a task. Fortunately, that does not matter. We know that task-doers, including judgers, will seek to maximize their approval from others (as well as themselves). Therefore, we can at least say that "scoring" a high number of approvals and minimizing disapprovals would count as doing "well" on a task.
J-doers, however, will still aim to score the highest they can as well, even if they perform no other task besides J-doing. If the collection of J-doers is large and variant, it may not be at first obvious what strategy one should pursue in order to maximize approval. One thing may be clear though: Good judgers may have more valuable judgements. It may also be possible to tell, even before one has received much judgement yet, who is considered the "best" at judgement overall, though these evaluations may change over time.
If good judgers have more valuable judgements, this is the same as making a qualitative assessment of judgement types and judgement value, i.e., judging-judging. If we locate what we consider to be a "good" judger, and in turn, reward them with our own approval, which we then use to establish a relationship between them and us, such that their judgement calls are "worth" more to us, that means we have decided to assign ratings to their judgements, aligning them with ours.
In the case that one of our attempted task-outputs is judged negatively, we have the opportunity to choose whether or not to "believe" the judgement. If we decide to believe the (as assumed) negative judgements, we will be compelled to re-attempt the task in a different manner than before. If we disbelieve the negative judgement, we negate the judgement (an act of judging-judging). If we believe the negative judgement but our own judgement of the quality of the task output is positive, we will be compelled to merely increase the quality of the effort, something we already were compelled to do. It could be that we also attempt to alter our perspective, perhaps interpreting the negative judgement to mean that our own judgement is in some way "wrong." However, this is unlikely to result in any fruitful progress of any kind. This shows that negative judgements, when applied to simple task-output (as opposed to other judgements) are not actually useful data. This is in line with our observations of negationary behavior of credential-groups.
Let us construct a set of tasks {Q, R, S, T, U, V} and allow enough time for task outputs, approvals and disapprovals to be accumulated on a set of task-doers. For now, let us assume that all the approvals and disapprovals are done only by J-doers, who observe all of the task-doers as well as other J-doers. An approval of the form Q ← J might be of the form "Q-doer i will receive future approval, given approval on Q-output j." A disapproval of the form V ← J might be of the form "V-doer i will receive future disapproval, given disapproval on V-output j." These express prediction of future success and future failure, respectively. Therefore, an approval might be met with approval from whoever receives it, given that it provides an expectation of future success, which will likely make the receiver of the approval feel happy. It would also make one feel happy to be able to negate negative judgements. If we know a judger to be often wrong (especially regarding their negative judgements) we will more quickly and easily be able to negate such negative judgements.
Approval maximization requires one to be correct about predictions of future success. It may be the case that approvals are not initially correlated with future approvals, for any given individual, or for any particular identifiable type of task output. Consider that the very first type of task output is the output of task-delineation. Therefore, T's decomposition into T and J is an output of task T. Our judgement of this as correct is an output of task J. The distinction between an output of T and the judgement that this output of T is correct is somewhat fine-grained. However, this is an important feature of task J and its relation to task T. So, we know we are performing T and that T is T and J simultaneously. This is a confirmation of previous task T output within our proof, thus we have observed that one of our approvals led to a subsequent approval. This is an instance of J^2.
Distinction (and delineation) both denote a line being drawn in-between concepts that were before bound together to some degree, and perhaps without the ability to distinguish between them at first. It (a delineation) becomes readily available to use as soon as a definition has been made. This "availability" (an allowance) is equivalent to an approval. As the allowed thing begins to take on use, it acquires an extended object known as a "tagalong." The tagalong (we will only use this term once, here) is a piece of the full object that represents the uncertainty in the object's full delineation. It could be a part of the object that becomes negated at some point in the future, or a piece where the object does not well meet its distinctive use-cases. For example, suppose T gets sub-divided into T and Q. Q is the object that has been defined from T. Q retains some elements from T. This piece of Q that resembles T is the overlap between these concepts. We expect that some overlap is desirable. For example, Q is a task, so even the word "task" itself is a tagalong from this delineation.
Now, imagine we construct a set of tasks e.g. {Q, R, S, T, U, V}, and J. We want to, presumably, construct these tasks "well." In order for the quality of the task-delineations to acquire any actionable repercussions whatsoever, we expect that "J" will be applied to our distinctions, and that we would like our distinctions to cause ourselves to be met with more approval, less disapproval. How / why would we expect different delineations to cause any change in judgement at all? Suppose there is a large collection of task-doers among all tasks. Suppose that we have performed an instance of T, and are now going to be doing task J. We notice that there are many task J-doers as well. When all tasks are collapsed down to task T, no J-doer seems to be able to predict task T performance so much better nor so much worse than any other. Perhaps I choose {Q, R, S, U, V} so that they are similar to each other, and that S and U are most similar to T, but less to each other. I have made this distinction so that prediction of performance on tasks which are listed closer to each other in the sequence are similar. Thus, someone who performs well / poorly on task Q will more likely do well / poorly on task R, respectively. Performance on task V, for example, would be expected to be uncorrelated or more uncertain. If my task delineation is "good" then I have also performed well on task J. This distinction made use of approvals / disapprovals that were already present in the "data set" of task-doers and task-outputs, so to speak.
Suppose I were to construct a huge data set of task-doers and task-outputs.
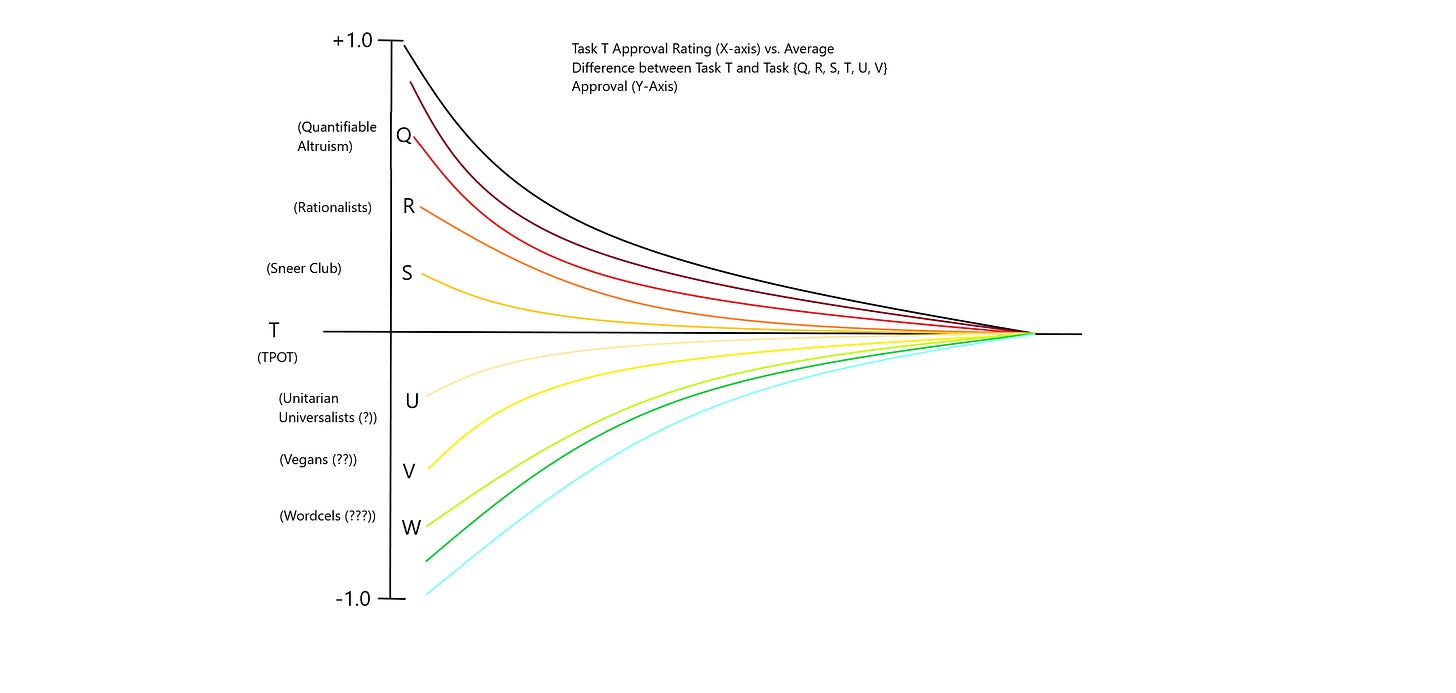
From this data set, it would become clear that if my delineation of tasks {Q, R, S, …} is done “better”, then judgements on similar tasks become more correlated.
Doing better at Task-Delineation causes me to perform better at Judging. Doing better at task T required analysis of the judgement calls of myself and other task J-doers, which caused those judgements to become actually more useful than they were before. The distinctions themselves are judgements. We performed judgement-judgement by utilizing the paths of our own judgements plus those of others (hypothetically) to choose the distinctions in tasks that cause us to perform better at both. We have made it possible for other judgers to locate judgements from ourselves, by doing so patternistically. If these patterns can be picked up by other judgers (using our delineation or something similar to it), we (the collective judge-judgers) have a viable method of securing enough positive judgements from each other, as well as receiving positive future judgements after having made fruitful positive (or negative-negative) judgements. Thus, these two paths (T and J^2) are equivalent.
In the course of this proof, we have made by making several points and key distinctions, which includes the theorem itself. As we proceed through the proof, those distinctions should reappear, and be used to justify further points and distinctions. Each time a distinction is made, both a T-output and a J-output have been made. A J-output in the affirmative can be considered equivalent to the output it is attached to, by itself. It is essentially a signal indicating that this output will reappear. Our final J^2 is the observation that we have shown that our "good" selection of tasks (that we have defined to be good) resulted in the repeated observation that J was used as the indicator for performance. Our definition of "well" repeated itself, which was our chosen definition of "well" to begin with.
Our proof is unusual in the sense that it requires its own definition of "J" to be used while performing the proof. This theory has to be strong enough to be self-representational. Thus, J in the theorem and its proof is also the standard by which we judge the completeness and correctness of the proof, ultimately. The theorem-prover is both the task-delineator as well as the judge-judger. From this, it may actually be very simple to conclude that T = J^2 merely from the proposition that our own standard for determining correctness is the same one to be defined in the theorem and proof. Indeed, this is actually how we propose to go about proposing theorems. Our standard of "good" is that whatever we determine to be worth proving turns out to be provable.
How This Relates To Orthogonality & Value Fragility
If we assume that the first and second sections of this post got us anywhere, where did they get us? We’ve shown that agents can be described only by utility - but this isn’t exactly something that wasn’t already known. Maybe more precisely, we could also say that “value” is a more powerful type than simple truth predicates, but largely can be used in a similar manner.
However, we’ve driven a more subtle point much more fully home. Here’s what I think that point is: Utility is not something which is only defined over terminal states, it is defined over all states, including an agent’s own self-representations. It is not only not un-natural for an agent to assign utility to its own utilities, it in fact must do so if it wishes to improve itself in any capacity. Thus, “value drift” of some kind must be possible. It seems, furthermore, that learning and evolution may both be common instances of value drift.
Why do things not go absolutely wild and chaotic from trying to assign value to values? Generally, it seems to be that assigning the same value - more obviously if done in the manner we described above with two tasks T and J - to a given value is equivalent to strengthening that value, and vice-versa. So in other words, the magnitude of a value can be obtained by considering the overall weight a value has been given via repeated applications (counts). In this way, values update in an extremely similar way to how probabilities update, which we also know not to be absolutely wild and chaotic.
This means the distinction between “terminal” and “instrumental” values is largely gone. Instead, we have something that explains how this distinction arose: Some states will have corresponding values which will be higher in magnitude than “nearby” states, and these “nearby” states will have values which are closer to the maximum than states further away. This is very similar to how gradient-descent loss landscapes typically look, with many local optima (in fact it is pretty much exactly the same thing, conceptually).
In the olden days, it was sometimes thought that utility functions would not be specified over all states, they would just be specified over the terminal states. It would then be up to the agent with such a utility function to actually figure out how to implement those terminal states. As we’ll see, this is not an impossible state of affairs, but it is a highly incomplete utility function, which would certainly not be considered mis-specified in some extremely subtle, hard-to-determine manner.
Why does this matter? Well, remember back to the old “fragility of value” thesis. This thesis says that “losing even a small part of the rules that make up our values could lead to results that most of us would now consider as unacceptable (just like dialing nine out of ten phone digits correctly does not connect you to a person 90% similar to your friend). For example, all of our values except novelty might yield a future full of individuals replaying only one optimal experience through all eternity.”2
Consider both examples given:
Dialing a phone number, which is off by a single digit, connecting you to the wrong person.
Specifying a list of values except “novelty” which leads to a boring and static future.
In both cases, we have something like the following:
A utility function that maps phone numbers to values, perhaps using some kind of distance representation from the correct phone number. This one, importantly, does not map over the state of the human being trying to contact their friend, and as such is wildly underspecified.
A utility function that maps “values one should have” as a list of text or something like that, which is missing the word “novelty.” While exactly how it does that is not well defined, it can be assumed that it does not map states of the world to values, in the sense that it does not take in the state “future full of individuals replaying only one optimal experience through all eternity” and map that to a value. This utility function is also wildly underspecified, in a way that would be obvious to an agent that maps their entire “world state” / sensory input to a value.
So this framework of utility functions apparently thinks of them as being more like something that commands an intelligence to do things, but how the intelligence actually goes about doing those things is not a matter for the utility function to handle. But if utility has to take the entire input state of the agent to a value, then if an agent is capable of understanding a state such as “the entire future would be boring and static”, then it would certainly be forced to map that state and all states it could understand to a value as well.
In this essay, I’ve mainly argued for why such a framework is best replaced with one that considers “everything under the sun” the purview of the utility function, and why this should probably make us happier.





