You're not (that) evil if you pick red

The short answer is that if you took this poll as a prior (for when Cremieux is asking), you should pick red.

[Update: full answer with o1 here.]

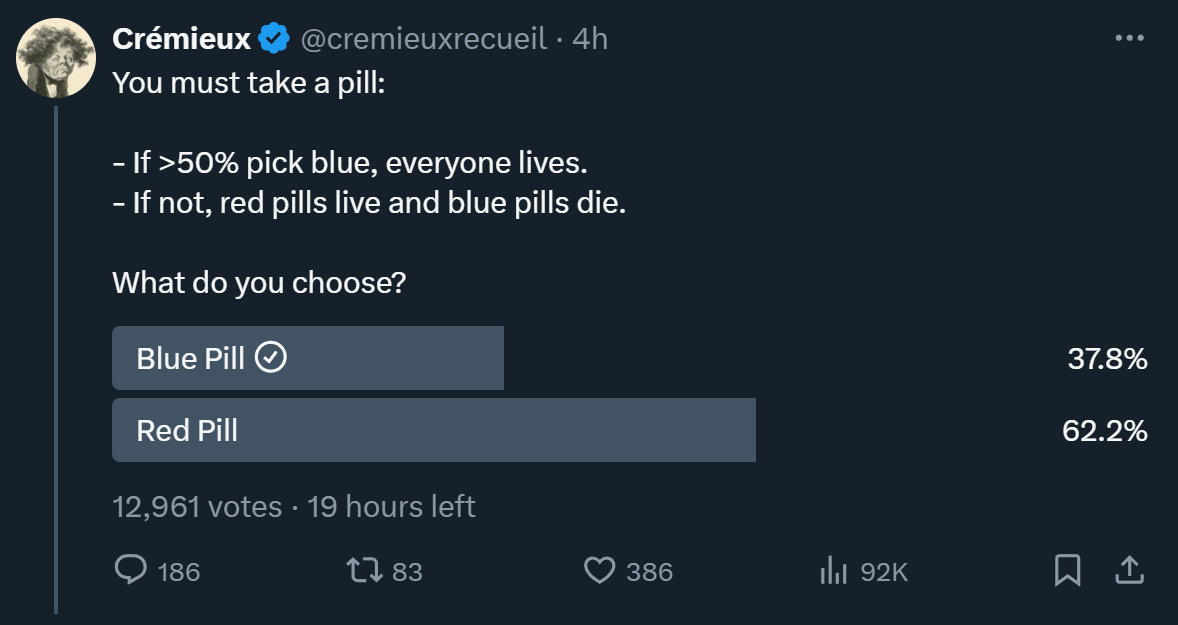
There’s a slightly utilitarian puzzle that sometimes crops up and is useful to test when conducting X polls. It is the one shown in the picture above.

The framing of it in terms of red and blue pills makes it seem somewhat more tribal than it actually can be, in the most abstract sense. Blue roughly vibes with “nice and dumb” and red with “mean but smart.”

In utilitarian terms, intuitively we should think that niceness can simply be represented by a parameter, which we’ll call v. This v is a number between 0 and 1 inclusive, so that 1 is the value of your own life, and v represents the value of any other human life.

If you’re perfectly evil, v = 0, and you should pick red. But if you’re not good enough to be perfectly evil, v > 0. However, what it should be seems very indeterminate.

Let’s consider what I’ll call the “CDT” case (your choice does not affect anyone else’s, and so only matters for a tiebreaker):

Let’s say N is the number of participants, and p is the probability a participant will choose blue. We’ll say x is the number of blues, sampled from a binomial distribution with parameters N and p.

There are only really three “worlds” you could find yourself in:

1. Red world, where red is guaranteed to win. Pick red in this one.

2. Blue world, where your choice does not matter. Pick either in this one, or blue to make sure it is even more certain.

3. The slim possibility that your choice changes the outcome, call this the tiebreaker world. It is assumed you will pick blue in this one.

Intuitively, it would seem that the expected utility you receive from your choice across all three worlds cancels out in the red and blue worlds, and so we should kind of only care about the chance of shifting the outcome in the tiebreaker world. (I am not going to write all those expectations out, since that would involve calculating really heavy integrals as far as I know, and I don’t think we really need them).

\(x \sim Binomial(N, p)\)

\(K = \lceil{}N/2\rceil{} - 1\)

\(p_{tie} = p(x = K)\)

\(p_{tie} = {N\choose K}p^{K}(1-p)^{N -K}\)

\(U_{saved} = p_{tie}Kv\)

You can see that as N gets larger, p_tie will get smaller, but K increases as well, so we’re not sure what this utility looks like.

But we can also see that for p small enough, that may outweigh whatever our v is.

For Cremieux’s poll at the time of that snapshot, we have N = 12,961, and - this would technically be for a subsequent poll - if you take this one as a prior for his community, then p = 0.378.

For these numbers, Wolfram Alpha tells me that p_tie is approximately 10^-175. So pick red.

However, for comparison, if his poll came out to close to 50/50, p_tie would be about 0.007. So U_saved would be approximately 45.36v.

Going through the above math with o1-preview, it tells me that in p = 0.5 situations, if

\(v > \sqrt{\frac{\pi}{2N}}\)

then pick blue. (I find the exact constant possibly dubious, but I’m more confident in the 1 / sqrt(N).)

To give a sense of how fast the probability of being in tiebreaker world drops off, with p of only 0.487, p_tie * K is 0.582, and with p of 0.488, that value is 1.11.

Now, I’m not going to do extended calculations for the FDT case, because it seems highly indeterminate what exactly happens here, besides one thing, which is that the probability of being in the blue world or the third world - the tiebreaker world - increases somewhat, with your choice (how you do that is also quite indeterminate, but perhaps through political campaigning, you can increase it a lot).

But suffice it to say, our conclusion is that red is the better choice if you’re fairly sure red will win (and it might be very sensitive to framing), and this won’t make you evil.

However, if N is very large, your v > 1 / sqrt(N), you have no other priors about p to go on, and you believe in FDT, then picking blue might seem quite justified. No one really knows what evil is besides v = exactly 0, and no one knows what the hell v is supposed to be.

But that’s what the praxis of utilitarianism is: The math tells you that your degree of evilness or goodness - based entirely on vibes and feeling - should come down to an arbitrary parameter of a very large number of significant figures. Then you go and reflect a long time until you pull this number out of absolutely nowhere, or wait until another calculation renders it non-arbitrary.