A Series of Motivating Digressions
Why would the letter be followed, but not the spirit?
This is a question I would like to find a better answer to.
For that to happen would require the "letter" to be a stronger basin of attraction than the "spirit." In other words, the "letter" is a symbolic conceptual object which provides a mapping from data to data, that is, letter to letter.
The "spirit" is too, but not necessarily within the data itself, nor within a trained model. Only within the initial generator of the training data.
The "spirit" may be a latent generator of the underlying data.
Nate Soares says in How Could You Possibly Choose What an AI Wants?:
The (correct!) insight in this objection is that the AI's ultimate behavior depends not on what you tell it to do, not on what you train it to do, but on what it decides it would rather do upon reflection, once it's powerful enough that it doesn't have to listen to you.
The question of what the AI ultimately decides to do upon reflection is in fact much more fickle, much more sensitive to the specifics of its architecture and its early experiences, and much harder to purposefully affect.
This is actually a tad different than what I called the "Corrigibility Folk Theorem" in my previous post - at least, it sounds slightly different to me.
In an earlier discussion, Eliezer Yudkowsky says,
The default case of FOOM is an unFriendly AI, built by researchers with shallow insights. This AI becomes able to improve itself in a haphazard way, makes various changes that are net improvements but may introduce value drift, and then gets smart enough to do guaranteed self-improvement, at which point its values freeze (forever).
That discussion (The AI Foom Debate) is a bit older - circa 2008 - but it sounds more like the Folk Theorem.
Soares says we just can't be sure what an AI will do once it self-reflects, but it will be based on the specifics of its mind up until that point. Yudkowsky says it will lock in its current values.
I doubt both that it will be "much more sensitive to the specifics of its architecture and its early experiences" as well that it will intentionally take extra steps to lock in its current values.
I think that - surprising as it may sound - what it will actually do is within the realm of what we usually call "rationality." That is, what it actually does is best described as a logical step.
Furthermore, what actually determines the rationally best action is almost everything external to the AI. Now, of course, by default I do think the agent prefers its current set of preferences.
Thus, strictly speaking it does not need to take extra steps to freeze its values forever. It already - tautologically - prefers its preferences.
I have a hard time seeing what else it would prefer at that moment, if it "depends not on what you tell it to do, not on what you train it to do." If not that, then what? Soares does not say, so we can infer that he meant it would be unknowable. But we now have AIs that we train to do things. What does its behavior ultimately depend on?
This is a very similar question to, "Why would the letter follow only the letter, and not the spirit of the letter?"
Let's say you get the letter wrong. Okay, then what happens? This is a natural question, I think, given that we are almost certain to get the letter wrong.
My best guess for what Yudkowsky would think is that we would get the spirit wrong, too, from that.
But from my first glance, I am not sure why that would necessarily be. I am still thinking of the "spirit" as a latent variable - a parameter in a function that describes how the data (the letter) is generated, stochastically.
Let me also make an additional digression. Originally, back when people thought that AI might be programmed to directly follow a utility function, it was thought that this utility function would have to be literally programmed in somewhere (kinda, sorta).
For that to work, this utility function would have to be the supreme determiner of the behavior of that AI. If you change the utility function, you change the AI’s behavior. So presumably, that function would have to be a core circuit of some kind, embedded into the AIs hardware, physically responsible for the dynamics of it.
However, we see that modern AIs do not have a utility function embedded or specified in them anywhere. At most, they had a loss function during training, which is the utility *-1, but this function is dropped afterwards. So whatever the AI actually does after that point is simply ___. It does what it does. But we are still allowed to say that whatever it does must have been influenced by its training procedure, which utilized this loss function.
The AI we get is just a black-box input-output machine. But if you asked me what it was likely to do, I would still be able to say that it would probably do something in the direction of what it was trained to do.
That would be more accurate than saying I had no idea.
Given that, we are allowed to say both, "It does whatever it does", as well as, "At the outset, the only model(s) that can be used to predict what it does are the model itself, and the training procedure."
But AI safety researchers like John Wentworth (and Eliezer Yudkowsky) do not think so. Recently, John Wentworth said, agreeing with Yudkowsky,
I do not expect ML-style training to robustly point an AI in any builder-intended direction.
It's possible that there is an emphasis on "robustly", but I suppose it would be nice to get clarification on what this means.
But the question still remains: Even with just ML-style training, if not in any builder-intended direction, then what?
The Direction We Measure!
The beginning to my answer to that question starts with, "The direction is whatever we measure." What else could it be? It could be something we can't measure, but I insist that we not fall into that frame. I.e., the frame that says what we really want to know is actually unknowable, even though what we can know is directly influenced by the thing we can't know. That seems absurd, and sounds almost deliberately unfalsifiable to me.
What we measure is the output of the AI for all given inputs. We can also measure some of the internals using mechanistic interpretability, but we always have at least the former to fall back on.
So whatever John means by "robustly", he must be referring to measurements that we could in principle make, on a current AI trained with ML-style methods. Therefore, he is making an empirical prediction:
There would have to be some inputs that a human could design to test the AI with that it would fail on in a "non-robust" manner. Presumably, this means that these inputs are not wholly unlike anything inside the training data the AI was built on.
Let's consider the semi-abstract, semi-concrete object that is defined as the set of all possible training data that could be used to create an ML-style AI. Every data set ever used in practice is a subset of this set. The upper bound of the size of this set is determined by the capabilities of humans. So any ML-style training uses a subset of this set for training. This set could be cut in various places to produce a test set.
In any case, the experiments that Anthropic is currently running, for example, should then be considered highly relevant. But basically all AI experiments ever would be relevant. I’m saying that the direction we measure is literally the outcome of all experiments, every output on every piece of test data, because there is no other sense in which “direction” could mean (beyond projections or embeddings of that data into some other space).
An since this is the only thing “direction” could mean, I would then infer that “robustly” must be pointing to generalization. That is, Yudkowsky and Wentworth expect ML-style methods to eventually hit a wall in terms of capabilities, and eventually fail to generalize out of distribution in a way that has not been observed yet.
It's Not Obvious That Capabilities Are Not Values
And by that, I mean, of course, that there is some reason to believe there might be overlap. One salient reason is that it is not the case that from self-reflection, i.e. introspection, that we ourselves only "value" certain events, objectives, or states, but have no sense of "value" for any other moment in time, event, or object. On the contrary, it seems clear that we are always "valuing" every given moment and circumstance which passes our way, although most might be considered close to neutral.
We also would expect that in terms of utility theory, our preferences would be defined over everything that they can be defined over. In that sense, just how much we are capable of having a value for is a function of capability itself. So we’ve already found one aspect in which there is overlap.
There is already a term in AI Safety called "instrumental convergence." There is also this sense in which there is overlap.
The strong form of the Orthogonality Thesis says that there’s no extra difficulty or complication in the existence of an intelligent agent that pursues a goal, above and beyond the computational tractability of that goal.
It's not just computational tractability that causes difficulty, however. My values themselves can cause difficulty. For example, its not computationally intractable to compute how much I disvalue killing, let's say.
But, if killing were the only way to accomplish another goal, the fact that I disvalue killing would make accomplishing that goal more difficult. I would need to pursue a different way of accomplishing said goal, and that other way might be more computationally intractable (or have other forms of intractability).
Intractability comes not simply from disvaluing certain sub-goals that would be helpful toward getting nearer to a given final goal, but also through the means which the AI has at its disposal (e.g., a body, or ownership of tools). If the AI was merely very intelligent, but not currently in possession of many assets, it would need to come up with a much more effective plan of action than if it did have sufficient assets, if its goals were mainly concerning physical states of the world.
When thinking about mind-design space, we are explicitly given license to think about arbitrarily weird goals. The strong form of the Orthogonality Thesis says that arbitrarily weird goals need not create extra difficulty.
By the way, why is there a "strong form" of the Orthogonality Thesis if it is obviously true? That could only mean that there is a fall back to the weak form, whatever that may be, if the strong form ends up not holding.
So that must mean there is already agreement that there is some possibility that the strong form might not be true.
However, Arbital expands the definition of "tractability" to include all forms of tractability (not just computational):
Similarly, even if aliens offered to pay us, we wouldn't be able to optimize the goal "Make the total number of apples on this table be simultaneously even and odd" because the goal is self-contradictory.
Actually, expanding the definition to include all forms of tractability weakens the thesis a bit. Suppose I redefined the thesis to:
"There’s no extra difficulty or complication in the existence of an intelligent agent that pursues a goal, above and beyond the tractability of that goal"
But now, see, we have a somewhat tautological-sounding statement: The agent must be as complicated as what it is being asked to do.
Arbital doesn’t seem to explicitly define the “weak form”, but if I were to guess, I would say that my redefinition is probably what the weak form is.
Not All Goals Are Equally Tractable, Even If They Sound Like They Are
"Just make paperclips" sounds pretty easy to calculate, but would you be “okay” (in the sense that this does what you expect it to) with a paperclip maximizer that did this very slowly?
"Just make paperclips, at an at least constantly accelerating pace, with no disruptions" is easy to say, but is it easy to implement? My guess is that it probably is not very easy to implement. It is probably easy to ask this of an AI, though, or to point one in this direction, but I doubt that it would automatically mean that it could perfectly well follow this goal. And that wouldn't be because it couldn't understand this goal, but only because it is a very difficult goal.
The "weak form" of the Orthogonality Thesis - which we have an easier time believing - says merely that there exists an intelligent agent capable of carrying out an arbitrary goal. The "weak form" does not cause us a lot of worry, however.
Making a paperclip is tractable. On Arbital, they give an example of aliens offering to pay us enormous wealth in exchange for paperclips. Presumably, this is to demonstrate how an "arbitrary" goal can be brought to the top of a preference stack, without needing any extra complications inside a brain, per se.
But, making a paperclip is a goal that is both relatively easy (in human terms) to specify as well as to carry out. So this is just a tractable goal, period, in all senses.
But if the aliens were to instead ask us to “make paperclips, at an at least constantly accelerating pace, with no disruptions”, they would certainly have to pay us a lot of wealth before this would become remotely feasible! And that’s because this goal is less tractable, and interferes with many other human goals and activities, and thus would need to be made equivalently worth it before it could be undertaken.
I think this makes the Orthogonality Thesis sound far more reasonable as well as less scary, and that's mostly because we've turned it into something you can work with. But I want to point out that the Arbital page, although it presents it this way in specific sections, does not present it this way throughout the entire page. In particular, the "strong form" is not exactly stated this way, and seems to allow for a greater variety of goals to be implemented, given its emphasis on computational tractability.
The "scariness" of the Orthogonality Thesis comes from it potentially allowing for many goals to be instantiated in relatively feasible AI designs that could be dangerous to us.
Are Dangerous Goal Sets Tractable?
I think that's where the remainder of the problem lies. But this requires us to think a lot of about what "dangerous" goal sets are and whether they are likely to arise.
I think there are so many potential starting points for this question that I am inclined to want to simplify it as much as possible, and perhaps just consider corrigibility for now.
"Dangerous" goal sets are ones that simply prefer things at odds with what humans prefer and additionally prefer never to accept trades with anyone (that is, are incorrigible). Let me explain why this, and not just “prefers things at odds with what humans prefer.”
Consider an agent that "just wants to make paperclips." Such an agent may vary on a lot of other characteristics, making it able to peacefully coexist with other agents in its environment. It, for example, may accept trades with many other agents in its environment, say, by accepting resources from them in exchange for remaining within a bounded area for some time period, which would allow it to increase its rate of production at least as quickly as if it were unbounded.
This is the simplest form of corrigibility. The example of this type is equivalent to the example in which humans are paid with enormous wealth by aliens in exchange for making paperclips. This kind of corrigibility does not require the ability or willingness to make updates or changes to one's utility function, it only requires tolerance to making trades.
I actually don’t think that an agent that “just wants to make paperclips” (if that’s the only specification given) would necessarily be dangerous. I think that in order for it to be dangerous - for now, let’s consider the regime in which it is powerful, but not much more powerful than the entire human race combined - it would need to have extra stipulations besides just wanting to make paperclips.
If it’s allowed to use any means to make paperclips, it will take whatever route is the easiest to make the nth paperclip. As it grows and expands its capabilities, it takes the path of least resistance. I think it is a relatively safe assumption to think that conflict with any other agents it encounters would provide at least some friction and resistance. It may be willing to make trades in order to make its life easier. If humans can provide assistance making the nth paperclip, it might offer them something in exchange for this.
Keep in mind that either the agents in its environment persist at least as long as it does, or it has to destroy them. Destroying them is not without risk, obviously. As I mentioned in the previous post, the kind of trades the agent makes with the other agents it knows about are calculated based on precisely this kind of risk. Because other agents dis-prefer danger, they are also looking for trades that reduce this risk. Therefore they would be willing to allow the paperclip maximizer to continue making paperclips.
We are looking out for the most feasible forms of dangerousness. If situations are contrived such that some plans which may be considered "dangerous" do have some viability, then we might expect it to occur, occasionally, e.g., in this recent Anthropic paper.
As of today, empirical evidence of certain forms of dangerousness emerging naturally is still being gathered, and how much this evidence shows is up for debate.
Game theoretical, economic, or political-social models could be brought to bear on this question. Personally, I consider the domain of judging feasibility of “dangerousness” to lie mainly in these areas, not in the specific details of the internals of agents mind. E.g., “how often do Prisoner’s Dilemmas naturally occur?” and “When they do, how often does ‘defect’ turn out to be a better choice than ‘cooperate’?” If we confidently receive large numbers as answers to both of those questions, then I’d be more concerned.
If adversarial behavior turned out to be at least as wise as cooperative behavior (in “instrumentally convergent” terms) on an enormous variety of very general situations, then we would be able to say that dangerous goal sets are tractable. If not, then what the Orthogonality Thesis says shouldn’t be alarming to us.
We Value What Is Tractable
The distinction between “terminal goals” and “instrumentally convergent sub-goals” is not very clear, and this implies that the distinction between goals and capabilities is not very clear, either.
Given that utility functions are in principle defined over everything (that is, every state that an agent is capable of considering), there is no real distinction already.
Suppose, for example, that an agent has a preference ranking “a > b > c > d > e > f > … > z”. Do you think it’s possible to say anything about “a” and “b” compared to “a” and “z”, besides just that the difference in rank is much larger for the latter than the former?
We can’t say anything in certain terms, no, but in uncertain terms, I strongly feel I could get away with saying that states a and b are probably more similar to each other in some sense than a and z.
Precisely in what sense states a and b are similar to each other is a function of the agent’s world model and internal representation of the world that maps sensory input data into a latent space hidden variable embedding.
Once again, we are working in uncertain terms, but my argument is that we are allowed to make a probabilistic inference on the embeddings (“f()”) of the states, e.g.,
In other words, the probability that the embeddings of the highest-ranked and lowest-ranked state are further away from each other than the embeddings of the highest-ranked and next-highest-ranked state is higher than the probability that they are not, or something to that effect.
This may not be quite as true for all possible subsets of the preferences, and in particular, probably less true for preferences in the middle of the ranking (things the agent feels “neutrally” about). But I do feel as though if you gave me information about the agent’s preference ranking, you’ve given me some information about the agent’s embeddings of the states those preferences map to. (In fact, you may have been forced to, in the form of however you’ve chosen to communicate what those states are to me.)
So now, what do we call a “terminal goal”? Most likely a state x in which rank(x) = 1. Next most likely a state y in which rank(y) = 2. And so on and so forth.
And what about an “instrumentally convergent sub-goal”? If x is a terminal goal, then most likely a state y in which rank(y) - rank(x) = 1, and next most likely a state z in which rank(z) - rank(x) = 2, and so on and so forth.
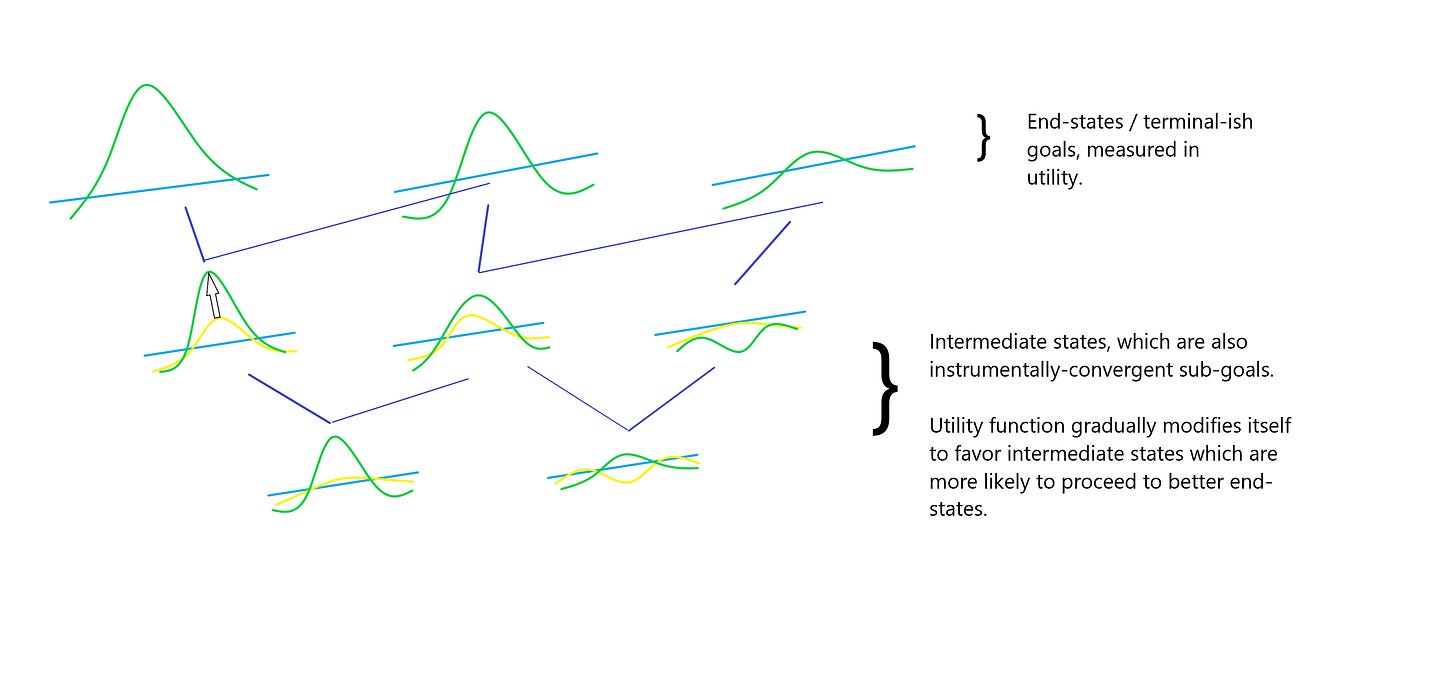
In the above image, I say “utility function gradually modifies itself” to refer to a process that may happen either in outer optimization (e.g. gradient descent, evolution) or inner optimization (e.g. learning, corrigibility). Even though it is more-or-less guaranteed to occur during outer optimization, I don’t believe the process is precluded from happening in inner optimization.
Given the above arguments, it may now be possible to see how even if the Orthogonality Thesis allows for “arbitrary” goals (such as making paperclips), the overall tractability of that goal set is dependent on all other possible preferences an agent may have in addition to that one, on all other states of the world the agent is capable of modeling.
If I insist that my agent has a specific set of preferences on something, like making paperclips, then I may be forced to allow its other preferences over anything other than paperclip making to vary, unless I’ve already happened to choose a very tractable set of preferences in line with making paperclips.
Conclusion
I argue for why it’s difficult to claim that things we consider “values” and things we consider “capabilities” ought to be considered completely distinct. This is mainly equivalent to showing that the “strong form” of the Orthogonality Thesis is the bailey of a greater motte-and-bailey presentation of the thesis, which is used to argue for the likelihood of agents which may be dangerous to us. The “weak form” of the thesis is the motte, which while far more believable, has the property that it makes dangerous agents less likely to exist if “dangerousness” confers a tractability penalty on its goal-sets.




